二分探索木をGoで実装してみた

はじめに

先日、7~9月に読んだ本をまとめていたところ、技術書を読めていないことに気づいた。

まだ自分はエンジニアとしては4年目でインプットを疎かにするには早すぎるので、この四半期はちゃんと技術書を読もうと心に誓った。今年はDBに強くなろうと思っていた年始の初心を思い出し、『詳説 データベース』を読み始めた。

第2章ではミュータブルなストレージ構造としてBツリーの基本を扱っており、その最初に二分探索木の解説があった。自分の中での理解を確かめるためにも言語化とGoによる実装をやっておきたい。

二分探索木

二分探索木とは

「二分」という名前の通り、二分探索木は各ノードが2つまでの子ノードを持つ木構造。英語だとBinarySearchTree, 略してBSTとも言う。

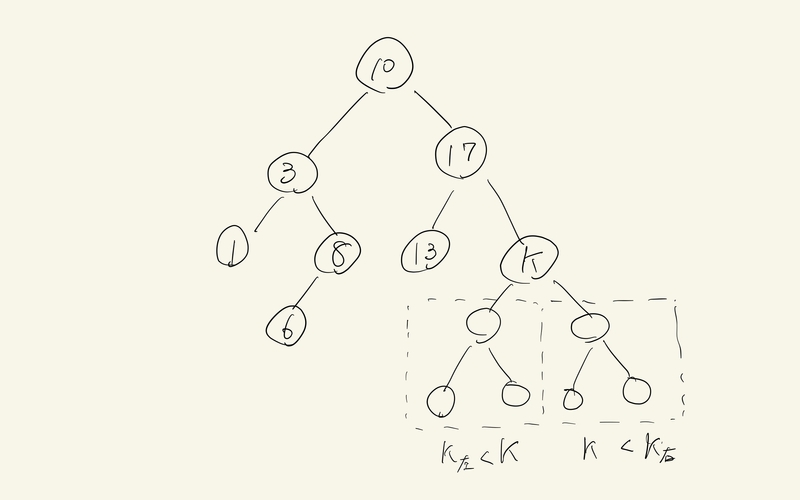
各ノードはキーによって表され、これに値が紐づけられている。親ノードのキーは左側のサブツリーに格納されているすべてのキーより大きく、右側のサブツリーに格納されているすべてのキーより小さい、というのが大きな特徴。同じ値のキーを許容する・しない、許容する場合は左右どちらのサブツリーに格納するかは要件次第。

ノードの挿入処理に特に決まりはないため、場合によっては枝の一方が他方より長くなる状況がありうる。こうなると検索時の計算量は線形となってしまう。

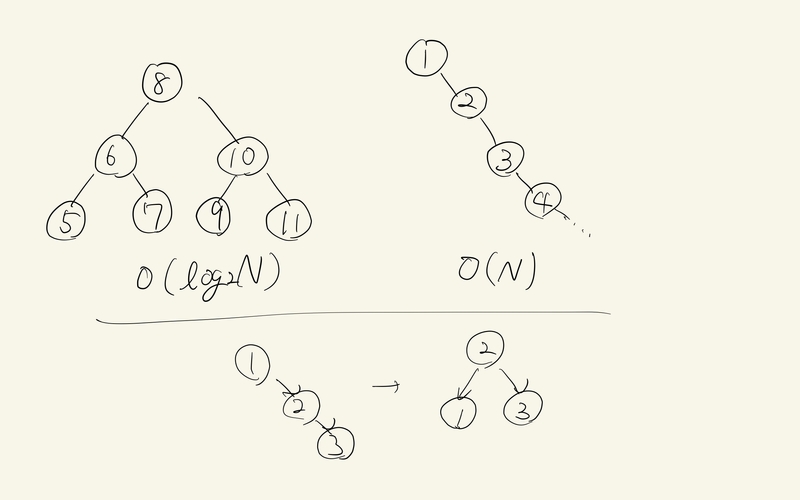
これを防ぐためにツリーのバランスを保つ必要がある。バランスが保たれたツリーは、Nをノードの総数としたとき高さが $log_2 N$ と定義される。このツリーにおける検索範囲は左右のサブツリーを辿ることで半分ずつになり、計算量は O($log_2 N$) という対数オーダーに収まる。

このバランスが保たれたツリーを維持するには、ノードの挿入・削除時にバランシング処理を行う必要がある。その一つの方法として回転操作がある。挿入によって子ノードを1つしか持たないノードが連続して並ぶことでバランスが保たれなくなったとき、中央のノードを中心として回転して親ノードとする。

ディスク上での問題点

二分探索木では検索計算量を O($log_2 N$) に収めるために、バランシングが必要となってくる。一方で、ノードが持てる子ノードの最大数であるファンアウトが2と小さいため、バランシング、ノードの回転といったノードの再構築処理を頻繁に行う必要があり、これをDBにおけるディスク上のストレージ用ツリーとして使うにはコストが大きくなり過ぎてしまう。

特に問題点としては2つあり、1つ目は局所性の問題。要素はランダムな順序で追加されるため、新しく追加されたノードがその親の近くに書き込まれることは保証されない。そのため、ノードの子ポインタが複数のディスクページにまたがってしまう可能性がある。

2つ目の問題としては子ポインタを辿る動作コスト。二分木においてファンアウトは2と小さいため、ツリーの高さは要素数の2進対数になる。つまり、ある要素の検索を行うには、ディスク上でのシーク操作を O($log_2 N$) 回実行する必要があり、ディスク転送も同じ回数実行する必要がある。

そこで、ディスク向けの実装に適したツリーには以下の特徴が必要となってくる。

• 大きなファンアウトを持ち、隣接するキーの局所性を改善する
• ツリーの高さを低く保ち、ノードを辿るときのシーク回数を削減する

実装

書籍内には実装コードはなかったのでGoで書いてみた。とはいえバランシング処理はなく、挿入・削除・検索といった簡単なもの。

実装コードは以下に置いておいた。

GitHub - okaryo/binary_search_tree_go: Go implementation of binary search tree

Go implementation of binary search tree. Contribute to okaryo/binary_search_tree_go development by creating an account on GitHub.

github.com

// データ構造
type Node struct {
	Value int
	Left  *Node
	Right *Node
}

type BST struct {
	Root *Node
}

func New() *BST {
	return &BST{}
}

// 挿入
func (bst *BST) Insert(value int) {
	bst.Root = insert(bst.Root, value)
}

func insert(node *Node, value int) *Node {
	if node == nil {
		return &Node{Value: value}
	}

	if value < node.Value {
		node.Left = insert(node.Left, value)
	} else if value > node.Value {
		node.Right = insert(node.Right, value)
	}

	return node
}

// 削除
func (bst *BST) Delete(value int) {
	bst.Root = deleteNode(bst.Root, value)
}

func deleteNode(node *Node, value int) *Node {
	if node == nil {
		return nil
	}

	if value < node.Value {
		node.Left = deleteNode(node.Left, value)
	} else if value > node.Value {
		node.Right = deleteNode(node.Right, value)
	} else {
		// 検索対象のノードが見つかったとき

		// 検索対象のノードが子ノードを持っていないとき
		if node.Left == nil && node.Right == nil {
			return nil
		}
		// 検索対象のノードが子ノードを1つだけ持っているとき
		if node.Left == nil {
			return node.Right
		}
		if node.Right == nil {
			return node.Left
		}

		// 検索対象のノードが子ノードを2つ持っているとき、右側サブツリーの最小値ノードで置き換える
		minLargest := findMinValue(node.Right)
		node.Value = minLargest
		node.Right = deleteNode(node.Right, minLargest)
	}

	return node
}

func findMinValue(node *Node) int {
	current := node
	for current.Left != nil {
		current = current.Left
	}
	return current.Value
}

// 検索
func (bst *BST) Search(value int) *Node {
	return search(bst.Root, value)
}

func search(node *Node, value int) *Node {
	if node == nil {
		return nil
	}

	if value == node.Value {
		return node
	} else if value < node.Value {
		return search(node.Left, value)
	} else {
		return search(node.Right, value)
	}
}

func (bst *BST) SearchMin() *Node {
	current := bst.Root
	for current.Left != nil {
		current = current.Left
	}
	return current
}

func (bst *BST) SearchMax() *Node {
	current := bst.Root
	for current.Right != nil {
		current = current.Right
	}
	return current
}

おわり

二分探索木は構造がシンプルで計算量が O($log_2 N$) とかなり有用に思ったが、ディスク上においてはいくつか問題点があった。それらの問題点を乗り越えるために今後の章ではBツリーやその亜種が出てくると思われる。それらも自分で言語化したり実装してみることでより深い理解を得られるようにしていきたい。

参考

• 『詳説 データベース』